| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Elasticsearch
- ES
- 누적합
- 완전탐색
- BFS
- 백준
- til
- programmers
- Generics
- 이분탐색
- 브루트포스
- 이분 탐색
- 객체지향
- Algorithm
- parametric search
- 일정 관리
- 구현
- 코딩테스트
- 계산기 만들기
- 해시
- SpringBoot
- 알고리즘
- binary search
- Baekjoon
- querydsl
- Spring
- 프로그래머스
- Java
- File
- 내일배움캠프
- Today
- Total
개발하는 햄팡이
[JAVA][백준 4948] 베르트랑 공준 본문
문제
베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다.
이 명제는 조제프 베르트랑이 1845년에 추측했고, 파프누티 체비쇼프가 1850년에 증명했다.
예를 들어, 10보다 크고, 20보다 작거나 같은 소수는 4개가 있다. (11, 13, 17, 19) 또, 14보다 크고, 28보다 작거나 같은 소수는 3개가 있다. (17,19, 23)
자연수 n이 주어졌을 때, n보다 크고, 2n보다 작거나 같은 소수의 개수를 구하는 프로그램을 작성하시오.
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
| 1 초 | 256 MB | 106973 | 41738 | 33392 | 38.543% |
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 케이스는 n을 포함하는 한 줄로 이루어져 있다.
입력의 마지막에는 0이 주어진다.
출력
각 테스트 케이스에 대해서, n보다 크고, 2n보다 작거나 같은 소수의 개수를 출력한다.
제한
- 1 ≤ n ≤ 123,456
예제 입력 1
1
10
13
100
1000
10000
100000
0
예제 출력 1
1
4
3
21
135
1033
8392자연수 n에 대하여 n보다 크고 2n보다 작거나 같은 소수를 찾는다는 문제 내용을 보고 바로 떠오른 것은 특정 범위내의 소수를 찾는 '에라토스테네스의 체'라는 방법이다.
엄청 특별한 건 없고 2부터 내가보려는 구간인 n까지 특정 수의 배수에 해당하는 수를 하나씩 지운다. 지울때 자기자신은 지우지 않는다.
에라토스테네스의 체라는 개념을 사용해야된다는 사실은 바로 생각났지만 구현이 문제였다.
입력값을 보면 계속 n값이 들어오다가 0이 들어오면 리턴을 하는데 입력받은 n마다 n에서 2n까지의 소수의 개수를 리턴해야한다.
처음 풀이로는
- 일단 input을 전부 받은 후
- 소수를 저장할 List를 만들고 이중for문을 돌면서 i가 j와 같지않으면서 i가 j로 나누어 떨어지지않으면 continue, 나누어떨어지면 break를 해주었고,
- cntArray를 만들어 배열의 index(현재 보는 수)보다 작거나 같은 소수의 개수를 전부 기록한다
- 마지막에 cntArr[num*2](2n보다 작거나 같은 소수의 개수) - cntArr[num](n보다 작거나 같은 소수의 개수)의 결과를 출력하였다.
그리고 시간초과가 났다.
↓ 실패한 코드 ↓
package S_4948;
// 베르트랑 공준
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
public class Main {
static int Max = 123456 * 2;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
ArrayList<Integer> input = new ArrayList<>();
while (true) {
int n = Integer.parseInt(br.readLine());
if (n == 0) {
break;
}
input.add(n);
}
ArrayList<Integer> decimalList = new ArrayList<>();
for (int i = 2; i <= Max; i++) {
boolean isDecimal = true;
for (int j = 2; j < i; j++) {
if (i % j == 0) {
isDecimal = false;
break;
}
}
if (isDecimal) {
decimalList.add(i);
}
}
// 어떠한 숫자 보다 작은 소수의 개수를 기록
int[] cntArr = new int[Max + 1];
cntArr[0] = 0;
int idx = 0;
int tmp = 0;
for (int i = 0; i < Max + 1; i++) {
int curNum = decimalList.get(idx); // 소수
// 현재보고있는 소수가 i보다 크면
if (i < curNum) {
cntArr[i] = tmp;
} else { // idx번째 소수가 i보다 작으면
if (idx + 1 < decimalList.size()) {
idx++;
tmp++;
cntArr[i] = tmp;
} else {
cntArr[i] = tmp;
}
}
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < input.size(); i++) {
int num = input.get(i);
sb.append((cntArr[num*2] - cntArr[num]) + "\n");
}
System.out.println(sb);
}
}

그런데 생각을 해보니깐
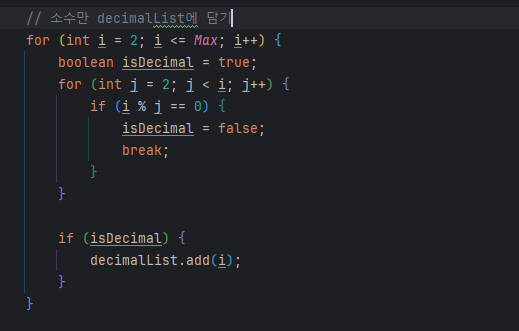
이 코드는 에라토스테네스의 체로 소수를 구한게 아니지 않나..?
왜 그 방법을 생각해놓고선 코드는 이렇게 구현한건지 잘 모르겠다.
에어컨이 고장나서 너무 더운 와중에 문제를 풀려고 하니깐 머리가 안돌아가서 그런 것 같다.
그래서 다시 일단 배열에 1부터 MAX*2만큼 담은 다음 2의 배수를 쭉 지우고 3의 배수를 쭉 지우고,, 이런 방법으로 소수만 남겨봤다.

테스트케이스를 돌려봤는데 엄청 오래걸리는 것 같은 느낌이 든다. 애초에 모든 수마다 해당 수보다 작거나 같은 소수의 개수를 기록해준 것이 문제 인 것 같았다. 어디서 오래걸리는지 찾기위해 중간에 "------------------------------"를 출력해봤는데 소수의 개수를 전부 기록하는 부분에서 잠시 기다려야했다.
그래서 그냥 소수 리스트를 정렬한 후 쭉 돌면서 n보다 크고 2n보다 작거나 같은 소수의 개수를 계속 세는 방법으로 바꾸었다.
근데 애초에 숫자를 차례대로 넣어서 정렬할 필요가 없어서 그냥 정렬은 안했다.
또 시간초과 났다..

뭔가 ArrayList에 넣었다 뺏다 하는 것 자체가 문제인 것 같아서 boolean[] isNotDecimal이라는 배열을 만들고 idx를 숫자로 하는 소수 표를 만드는 방식으로 해보기로 했다.
세번째도 시간초과.....
결국 지인들의 해설을 들었는데 에라토스테네스의 체 개념 + 다른 수학적 개념(원리)들을 결합해서 풀었어야했다.
결국 실패....나중에 다시 풀어봐야겠다 ^^!!
풀이
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
public class Main {
static int Max = 123456 * 2;
static boolean[] isNotDecimal = new boolean[Max + 1];
static int[] cntArr = new int[Max + 1];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
isNotDecimal[0] = true;
isNotDecimal[1] = true;
// i: 나누는 수, j: 나누어지는 수
for (int i = 2; i <= Math.sqrt(Max); i++) {
for (int j = (int) Math.pow(i, 2); j < Max + 1; j += i) {
if (isNotDecimal[j]) {
continue;
}
// 나누어 진다면
if (j % i == 0) {
isNotDecimal[j] = true;
}
}
}
// 어떠한 숫자 보다 작은 소수의 개수를 기록
cntArr[0] = 0;
for (int i = 2; i < Max + 1; i++) {
if (isNotDecimal[i]) {
cntArr[i] = cntArr[i - 1];
} else { // 소수면
cntArr[i] = cntArr[i - 1] + 1;
}
}
ArrayList<Integer> input = new ArrayList<>();
while (true) {
int n = Integer.parseInt(br.readLine());
if (n == 0) {
break;
}
input.add(n);
}
StringBuilder sb = new StringBuilder();
for (int i = 0; i < input.size(); i++) {
int n = input.get(i);
sb.append((cntArr[n * 2] - cntArr[n])).append("\n");
}
System.out.println(sb);
}
}'Algorithm > Baekjoon' 카테고리의 다른 글
| [JAVA][백준 3085] 사탕 게임 (2) | 2024.06.11 |
|---|---|
| [JAVA][백준 11068] 회문인 수 (0) | 2024.06.10 |
| [JAVA][백준 11005] 진법 변환2 (1) | 2024.06.10 |
| [JAVA][백준 10448] 유레카 이론 (0) | 2024.06.08 |
| [JAVA][백준 2309] 일곱 난쟁이 (0) | 2024.06.03 |


